Ostatnim elementem modelu elektrowni wiatrowej jest model generatora, który często tworzy się wraz z modelem systemu elektroenergetycznego, co pozwala na szczegółową analizę parametrów energii elektrycznej oddawanej do sieci przez siłownię wiatrową. Struktura takiego modelu zależy od zastosowanego rozwiązania, i wiąże się z typem wykorzystanego generatora (synchroniczny lub asynchroniczny), rodzajem pracy (wyspowa bądź współpraca z siecią operatora) oraz podłączeniem do sieci (bezpośrednio czy przez przekształtnik energoelektroniczny). Ponieważ tematem pracy dyplomowej jest model silnika wiatrowego, a nie generatora do zamodelowania tego elementu podchodzi się w sposób uproszczony. Związku z tym, że procesy dynamiczne zachodzące w generatorze są znacznie szybsze niż w silniku wiatrowym, postanowiono przyrównać dynamikę generatora do członu inercyjnego pierwszego rzędu ze stałą czasową wynoszącą (1):

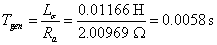(1)

gdzie:

Lσ - indukcyjność rozproszenia, Ra - rezystancja twornika.

Dzięki uprzejmości firmy Komel, która odpowiedziała na zapytanie dotyczące parametrów generatora znajdującego się na stanowisku laboratoryjnym, możliwe było dokładne określenie stałej czasowej tego urządzenia (1). Następnie stałą tą zaimplementowano w modelu matematycznym. Dla tak zdefiniowanej dynamiki można przyjąć, że moc czynna P_g oddawana do sieci przez generator jest równa (2):

(2)

gdzie:

Pgzad - zadana moc generowana.

W celu zdefiniowania optymalnej metody sterowania generatorem należy powrócić do analizy wzoru zawartego w poprzednich podrozdziałach, którego postać ponownie zaprezentowano poniżej (3):

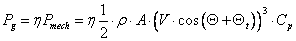(3)

Zakładając, że η = 87.7 % ρ = 1,225 kg/m3, Θ = 10^o, Θ_t = 10^o oraz jednocześnie znając przebieg funkcji C_p = ƒ(λ) (rys. 1) modelowanej elektrowni wiatrowej, można wyznaczyć rodzinę charakterystyk statycznych wytwarzanej mocy generatora P_g dla różnych prędkości wiatru V, w funkcji prędkości obrotowej koła wiatrowego ω_w. Na rys. 1 przedstawiono taką rodzinę z zaznaczeniem ekstremalnej krzywej mocy P_g^max. Krzywą tą wyznacza się, zakładając, że elektrownia wiatrowa pracuje w punkcie ekstremum funkcji C_p = ƒ(λ), w którym współczynnik wykorzystania energii wiatru osiąga swoją maksymalną wartość C_p^max = 0.412. Znajomość charakterystyki C_p = ƒ(λ) pozwala na wyznaczenie takiego prawa sterowania, które na podstawie zmierzonej prędkości wiatru dążyłoby do osiągnięcia punktu pracy leżącego na charakterystyce ekstremalnej krzywej mocy. Jednak w punkcie tym siłownia wiatrowa znajduje się na granicy stabilności. Gdyby w wyniku nieprzewidywalnych zjawisk punkt pracy przesunąłby się nieznacznie w lewo od punktu λ_optopt na charakterystyce C_p = ƒ(λ) moment oporowy generatora byłby większy od momentu mechanicznego pochodzącego od koła wiatrowego, przez co doszłoby do zatrzymania się wirnika turbiny. Jednocześnie sterowanie oparte na pomiarze prędkości wiatru, który ma charakter stochastyczny nie jest dobrym rozwiązaniem.

Rys. 1. Rodzina charakterystyk statycznych P_g = ƒ(ω_w,V) z zaznaczeniem ekstremalnej krzywej mocy.

Przy wyznaczaniu ekstremalnej krzywej mocy przyjęto, że sprawność generatora jest stała w całym zakresie pracy. Jednak w rzeczywistości wartość ta zdeterminowana jest przez występujące w maszynie straty, które ze względu na swoje pochodzenie można podzielić na straty mechaniczne oraz elektryczne. Dokładne rachunkowe wyznaczenie ich wartości jest skomplikowane, ponieważ niektóre z nich są proporcjonalne do prędkości obrotowej, inne za to zależą od kwadratu indukcji, z kolei pozostałe mają wartość stałą. Związku z tym na potrzeby modelu matematycznego dokonano pomiarów generowanej mocy, przy różnych prędkościach obrotowych maszyny, co pozwoliło wyznaczyć charakterystykę strat w funkcji prędkości. Tak otrzymane dane wykorzystano przy aproksymacji tej charakterystyki, czego rezultatem jest wzór (4):

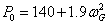(4)

gdzie:

P0 - moc strat.

Po wyznaczeniu strat powstających w generatorze możemy zapisać, że moment oporowy T_g pochodzący od tego urządzenia wyniesie (5) :

(5)

Powracając do układów sterowania pracą generatora, najczęściej stosowanym rozwiązaniem jest układ z pomiarem prędkości obrotowej, którego prawo sterowania opiera się na zasadzie (6):

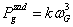(6)

gdzie:

k - współczynnik wzmocnienia.

Dla każdej elektrowni wiatrowej z poziomą osią obrotu istnieje taka wartość wzmocnienia k_opt, dla którego krzywa pracy turbozespołu pokrywa się z ekstremalną krzywą mocy i wynosi (7):

(7)

W rzeczywistych obiektach wartość współczynnika wzmocnienia k ustala się na poziomie nieznacznie mniejszym niż odpowiada to wzmocnieniu kopt. Wiąże się to z tym, że zmiana temperatury, gęstości powietrza czy nawet oblodzenie łopat wpływają na kształt krzywych mocy, przez co elektrownia wiatrowa dla zbyt dużego współczynnika wzmocnienia k mogłaby się znaleźć w niestabilnym punkcie pracy.

Opisane powyżej prawa sterowania opierają się na znajomości charakterystyki C_p = ƒ(λ). Jednak nie zawsze jest ona dostępna dla układu sterowania. Istnieje rozwiązanie, które w sposób ciągły poszukuje optymalnego wzmocnienia k_opt. Pozwala to pracować elektrowni w punkcie znajdującym się na ekstremalnej krzywej mocy. Algorytm ten realizowany jest za pomocą układu równań (8):

(8)

gdzie:

Δk - przyrost współczynnika wzmocnienia, ΔPgen - przyrost mocy generowanej przez generator, Δkzad - zadany przyrost współczynnika wzmocnienia.

Zasada działania tego algorytmu jest przedstawiona na rys. 2. Jak z niego wynika w przypadku kiedy współczynnik wzmocnienia wzrośnie z k₂ do k_opt (Δk>0) moc generowana również wzrośnie ( gen>0), powodując dodatni przyrost współczynnika wzmocnienia w kolejnym kroku (Δk_zad>0). Konsekwencją tego będzie przejście układu na krzywą mocy k₁. W tej sytuacji przyrost współczynnika wzmocnienia będzie dodatni (Δk>0), natomiast moc zmaleje (ΔP_gen<0). Jak wynika z układu równań (8) dla takich warunków przyrost współczynnika wzmocnienia w kolejnym kroku będzie ujemny (Δk_zad<0), w rezultacie czego nastąpi przejście układu z powrotem na krzywą k_opt. Przy zastosowaniu tego rodzaju nadrzędnego regulatora mocy należy odpowiednio dobrać wartość przyrostu współczynnika wzmocnienia w kolejnych krokach Δk_zad oraz okres impulsowania regulatora. W trakcie doboru drugiego parametru należy wziąć pod uwagę całą dynamikę procesu przetwarzania energii wiatru na energię elektryczną, którą w zależności od wielkości elektrowni należy liczyć w sekundach.

Rys. 2. Zasada działania algorytmu poszukującego ekstremalnej krzywej mocy.

Model matematyczny generatora z algorytmem poszukiwania krzywej mocy został zaczerpnięty z pracy [7]. Dokonano jego pewnych modyfikacji polegających na umieszczeniu go w masce podsystemu ”MODEL GENERATORA ZE STEROWANIEM”, co umożliwiło stworzenie okna dialogowego (rys. 4) pozwalającego na włączenie oraz wyłączenie algorytmu poszukiwania bez konieczności wchodzenia do wnętrza programu.

Rys. 4. Okno dialogowe maski podsystemu ”MODEL GENERATORA ZE STEROWANIEM”.