W przypadku kiedy koło wiatrowe ustawione jest dokładnie w pozycji prostopadłej do kierunku wiania wiatru, to środek parcia wiatru na silnik wiatrowy znajduje się w środku tego koła. Natomiast siła parcia dla takiego położenia turbiny wiatrowej, zawiera tylko jedną składową, prostopadłą do płaszczyzny koła (siła F_X). Jednak w momencie kiedy dojdzie do pewnego odchylenia płaszczyzny wirnika od położenia prostopadłego do wiatru, środek parcia przesunie się w bok o pewien odcinek l_x. W takim przypadku siła parcia w zawiera dwie składowe rys. 1:

Rys. 1. Siły aerodynamiczne, występujące na kole wiatrowym odchylonym od kierunku wiatru (Θ - kąt odchylenia osi wirnika od kierunku wiatru, Θ_z - położenie osi wirnika, Θ_wiatr- kierunek wiania wiatru, F_T - siła boczna wywierana przez wiatr na ster tylni, F_X, F_Y - składowe siły parcia wiatru na koło wiatrowe, V - prędkość wiatru, V_X i V_Y - składowe prędkości wiatru, V₀ - prędkość wiatru za kołem wiatrowym,V_0X i V_0X - składowe prędkości wiatru za kołem wiatrowym z - prędkość kątowa elektrowni względem osi pionowej Z, l_t1 i l_t2 - ramie siły F_T, l_ster - długość płata steru tylnego, l_x - ramie siły F_X , l_y - ramie siły F_Y).

Ze względu na złożoność występujących tu zjawisk rachunkowe określenie wartości składowych sił parcia jest bardzo skomplikowane. Dlatego też zazwyczaj wyznacza się je empirycznie w tunelach aerodynamicznych, a następnie przedstawia się na wykresach w postaci krzywych. Na ogół wykresy te nie przedstawiają wielkości sił, a jedynie wartość współczynników aerodynamicznych C_x oraz C_z.. Dla tak zdefiniowanych współczynników aerodynamicznych wartość składowych sił parcia wyniesie (1), (2):

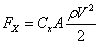(1)

(2)

Charakterystyki współczynników aerodynamicznych C_x oraz C_z w funkcji kąta natarcia wiatru na koło wiatrowe są zazwyczaj pilnie strzeżoną tajemnicą firm produkujących siłownie wiatrowe. Z tej przyczyny podczas przeszukiwania zasobów dostępnej literatury oraz Internetu nie znaleziono charakterystyk, które dokładnie odpowiadałyby modelowanej elektrowni wiatrowej. Niemiej jednak w publikacji [3] umieszczono wykresy współczynników aerodynamicznych dla silnika wiatrowego, które sporządzone zostały dla turbiny wiatrowej składającej się z czterech płatów (modeluje się elektrownię wiatrową o trzech płatach). Z braku innego zadowalającego rozwiązania postanowiono wykorzystać te krzywe zmienności współczynników aerodynamicznych. W związku z tym należy pamiętać, że otrzymane wyniki z symulacji modelu nie będą dokładnie odzwierciedlać rzeczywistości. Wypada jednak zaznaczyć, że charakterystyki te kształtem są bardzo zbliżone do silników wiatrowych o trzech płatach, tak więc dynamika nadążania elektrowni wiatrowej za kierunkiem wiania wiatru powinna być zachowana.

Przebieg zmienności funkcji współczynników aerodynamicznych C_x oraz C_z w zależności od kąta natarcia Θ przypomina kształtem przebieg funkcji wielomianowej (rys 2). Ta właściwość pozwala aproksymować charakterystyki wykorzystując do tego celu tylko dwa wielomiany (po jednym dla każdego przebiegu). Podobnie jak w przypadku zmiennej położenia środka parcia x_p^T do aproksymacji posłużono się matlabowską komendą polifit(). Cały skrypt umieszczono w zakładce Initialization w masce podsystemu ”MODEL STERU TYLNEGO ZE STEROWANIEM”. Rząd aproksymującego wielomianu dobrano tak, aby błąd aproksymacji nie przekroczył wartości +/-0.5% wartości rzeczywistej.

Rys. 2. Wynik aproksymacji charakterystyk współczynników aerodynamicznych C_x oraz C_y w funkcji kąta natarcia wiatru Θ (dla silnika wiatrowego z czteropłatowego), z zaznaczeniem punktów użytych do aproksymacji.

Z rys. 2 wynika że aerodynamiczny współczynnik osiowego parcia wiatru na koło wiatrowe C_x największą wartość osiąga przy prostopadłym ustawieniu koła wiatrowego względem kierunku wiania wiatru. Natomiast przy coraz większym odchyleniu turbiny wiatrowej od tego położenia współczynnik ten maleje. Z kolei przebieg współczynnika siły bocznej C_z jest zupełnie inny. Przy coraz większym odchyleniu silnika wiatrowego od wiatru, współczynnik ten rośnie, aż do osiągnięcia wartości maksymalnej, a później ponownie maleje. Należy zaznaczyć, że przebieg tej charakterystyki jest przesunięty w prawo o wartość kąta 0.17 rad.

Rachunkowe określenie wielkości sił F_X oraz F_Z pozwala obliczyć wartość momentu obrotowego wywołanego siłą parcia wiatru na koło wiatrowe. Moment ten będzie równy sumie momentów wywoływanych składowymi siły parcia. W przypadku składowej F_Y wyznaczenie wartości tego momentu jest prostym zadaniem, ponieważ ramie siły F_Y nie zmienia się i jest równe odcinkowi l_y łączącemu środek koła wiatrowego z osią obrotu gondoli (rys. 1). Tak zdefiniowany moment obrotowy wyniesie (3):

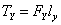(3)

Z kolei długość ramienia siły F_Y nie jest stała, lecz zmienia się wraz ze zmianą środka parcia wiatru na koło wiatrowe. Tym samym wielkość bocznego przesunięcia środka parcia (ramie siły) wyniesie (4):

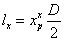(4)

gdzie:

xpx – współczynnik przesunięcia środka parcia wiatru na koło wiatrowe.

Podobnie jak w przypadku charakterystyk współczynników aerodynamicznych C_x oraz C_y nie udało się znaleźć przebiegu krzywych zmienności środka parcia wiatru na koło wiatrowe x_p^x wykonanych dla elektrowni wiatrowych posiadających trzy płaty. Wobec tego posłużono się charakterystyką zamieszczoną w publikacji [3], którą sporządzono dla turbin o czterech płatach. Wykres ten posiada wierzchołki, w których kąt nachylenia krzywych względem osi odciętych gwałtownie się zmienia. Natomiast pomiędzy tymi wierzchołkami wartość współczynnika środka parcia zmienia się zgodnie z funkcją liniowa. W związku z tym zdecydowano się dokonać oddzielnie interpolacji wielomianem pierwszego rzędu odcinków charakterystyki, które znajdują się pomiędzy tymi wierzchołkami. Natomiast resztę charakterystyki aproksymowano wielomianem wyższego rzędu. Funkcja x_p^x = ƒ(Θ) jest również funkcją parzystą, więc wystarczyło aproksymować ją tylko dla dodatnich argumentów kąta Θ. Podobnie jak w innych przypadkach do tego celu wykorzystano funkcję polifit(). Cały skrypt umieszczono w masce podsystemu ”MODEL STERU TYLNEGO ZE STEROWANIEM”. Na rys. 3 przedstawiono wynik dokonanej aproksymacji oraz interpolacji z zaznaczeniem punktów użytych do tego celu. Jak widać w przypadku odcinków, w których dokonano interpolacji funkcja przechodzi dokładnie przez wierzchołki charakterystyki przez tzw. węzły interpolacyjne. Natomiast w przypadku odcinka, w którym dokonano aproksymacji wykresu można zauważyć niewielki błąd aproksymacji, który nie przekracza wartości +/-0.5% wartości rzeczywistej.

Rys. 3. Wynik aproksymacji charakterystyki współczynnika przesunięcia środka parcia x_p^x (dla silnika wiatrowego czteropłatowego), z zaznaczeniem punktów użytych do aproksymacji.

Po zdefiniowaniu długości ramienia składowej siły parcia F_X możemy określić, ile wyniesie moment obrotowy pochodzący od tej składowej siły (5):

(5)