Model wiatru - moc wiatru a moc turbiny
Energia kinetyczna zawarta w powietrzu o masie m poruszającym się z prędkością V określona jest wzorem (1):
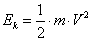 |
(1) |
Natomiast moc przepływającego powietrza przez powierzchnię zakreślaną przez koło wiatrowe wynosi (2):
 |
(2) |
gdzie: |
ρ - gęstość powietrza,
A- pole powierzchni zakreślone przez płaty wirnika,
V- prędkość powietrza. |
Jak wynika ze wzoru moc przepływającego powietrza jest wprost proporcjonalna do gęstości powietrza, powierzchni zakreślanej przez łopaty wirnika oraz do sześcianu prędkości wiatru. Energia kinetyczna przepływającego powietrza nie może być całkowicie odbierana powietrzu, dlatego też prędkość wiatru za wirnikiem nie wynosi zero, ale porusza się ze zredukowaną prędkością. Rzeczywista energia pobierana przez łopaty turbiny wiatrowej jest związana z różnicą prędkości przepływającego przez wirnik powietrza i określona jest wzorem (3):
 |
(3) |
gdzie: |
V - prędkość wlotowa powietrza,
V0 - prędkość wylotowa powietrza. |
Zatem moc mechaniczna pozyskiwana przez wirnik, który napędza generator, wynosi (4):
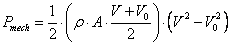 |
(4) |
Powyższe wyrażenie (4): można przekształcić na postać algebraiczną (5):
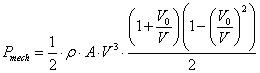 |
(5) |
Moc uzyskiwana przez płaty wirnika jest zazwyczaj przedstawiana w postaci (6):
 |
(6) |
gdzie: |
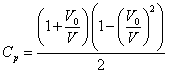
|
(7) |
Wyrażenie (7) jest współczynnikiem wykorzystania energii wiatru. Dla danego wiatru wiejącego w stronę wirnika, wartość współczynnika Cp zależy od stosunku prędkości wiatru przed i za wirnikiem (V0/V). W przypadku gdy wiatr za turbiną wiatrową osiąga prędkość trzy razy mniejszą w stosunku do prędkości wiatru przed wirnikiem, współczynnik Cp osiąga swoją maksymalną wartość 0.593 (tzw. limit Betza). W rzeczywistych konstrukcjach ze względu na powstające w turbinie wiatrowej straty aerodynamiczne maksymalnie udaje się osiągnąć niewiele ponad wartość 0.4 (dla współczesnych trójpłatowych silników wiatrowych z poziomą osią obrotu).
Jak wynika ze wzoru (6) moc mechaniczna turbiny wiatrowej jest wprost proporcjonalna do gęstości powietrza, która powiązana jest z ciśnieniem, temperaturą oraz z wilgotnością .W obliczeniach często przyjmuje się wartość 1,225kg/m3 odpowiadającą gęstości powietrza na poziomie morza przy ciśnieniu jednej atmosfery (1,03kg/cm2) i temperaturze 15oC.
W równaniu mocy (6) można również zauważyć, że moc osiągana przez turbinę wiatrową jest wprost proporcjonalna do powierzchni zakreślanej przez wirnik. Dla turbin z poziomą osią obrotu powierzchnia ta wynosi (8):
 |
(8) |
gdzie: |
D - średnica wirników turbin. |
Wyrażenie (7) Powierzchnia zakreślana przez wirnik turbiny wiatrowej determinuje jak dużo energii można uzyskać w ciągu roku z danej elektrowni. Biorąc pod uwagę, że praca turbin wiatrowych jest zoptymalizowana dla pewnych prędkości wiatru (zazwyczaj mieszczących się z zakresie 11-17 m/s) możemy określić jak średnica wirnika wpływa na moc generowaną przez elektrownię. Rys. 1 przedstawia pewne wyobrażenie tego, jaką wartość mocy może uzyskać elektrownia wiatrowa w przypadku typowych wielkości wirnika. Jednak nie jest on obowiązującą regułą, ponieważ często firmy przy produkcji silników wiatrowych optymalizują ich punkt pracy ze względu na miejsce, gdzie ma się przyszła elektrownia znajdować.
Rys. 1. Średnice wirników i odpowiadająca im moc.
|

