Na potrzeby modelu matematycznego przyjęto, że ster tylni elektrowni wiatrowej jest sterem prostokątnym o długości l_ster, a szerokości dwa razy mniejszej od długości. Wymiar ramienia l_t1, na którym zamontowano ster równa się średnicy koła wiatrowego D. Założenia te pozwalają na oszacowanie siły wywieranej przez wiatr na ten element układu. Powierzchnia tak zdefiniowanego steru wynosi (1):

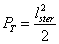(1)

Aerodynamiczna siła wywierana przez wiatr na ster tylni równa się (2):

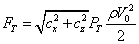(2)

gdzie:

cx - aerodynamiczny współczynnik oporu profilowego, cz - aerodynamiczny współczynnik siły nośnej.

Wartość współczynników aerodynamicznych c_x i c_z w znacznym stopniu zależy od kształtu steru oraz kąta natarcia strumienia wiatru Θ. Zazwyczaj wyznaczane są one doświadczalnie podczas odmuchiwania profilu dla różnych kątów natarcia.

Wcześniej zdefiniowany ster tylni można przyrównać do płata o profilu płaskiej płyty z wydłużeniem wynoszącym λ_w=0.5 (stosunek szerokości steru do długości). W publikacji [1] podano że dla takiego profilu o nieskończenie dużym wydłużeniu współczynniki aerodynamiczne w funkcji kąta natarcia można aproksymować funkcjami (3), (4):

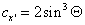(3)

(4)

Tak zdefiniowany aerodynamiczny współczynnik oporu profilowego c_x' (3) nie uwzględnia zjawisk zachodzących na końcach profilu. Powstające tam zawirowania spowodowane wyrównywaniem się ciśnień na górnej i dolnej powierzchni płata powodują powstawanie tzw. oporów indukowanych. Z teorii oporu indukcyjnego wynika że współczynnik oporu indukcyjnego wynosi (5):

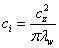(5)

gdzie:

λw - wydłużenie.

Zatem całkowity aerodynamiczny współczynnik oporu czołowego profilu c_x dla steru tylnego składa się z sumy dwóch współczynników i wynosi (6):

(6)

Na rys 1 przedstawiono wartość aerodynamicznych współczynników oporu indukcyjnego c_i, oporu profilowego c_x oraz siły nośnej c_z w funkcji kąta odchylenia osi wirnika od kierunku wiania wiatru Θ. Należy zaznaczyć, że wartość tych współczynników jest identyczna dla ujemnych jak i dodatnich kątów Θ (funkcja parzysta). Własność tą wykorzystano w modelu matematycznym, gdzie zamiast tworzyć dwie odrębne funkcje do liczenia wartości współczynników aerodynamicznych dla kątów dodatnich bądź ujemnych, stworzono jedną funkcję, której argumentem jest wartość bezwzględna kąta Θ.

Rys. 1. Wartość aerodynamicznych współczynników oporu indukcyjnego c_i, oporu profilowego c_x oraz siły nośnej c_z w funkcji kąta odchylenia osi wirnika od kierunku wiatru Θdla profilu płaskiej płyty o wydłużeniu λ_w=0.5.

Siła wywierana przez wiatr na ster tylni, jak wynika ze wzoru (2), jest wprost proporcjonalna do prędkości wiatru za kołem wiatrowym V₀. Prędkość tą można oszacować, przekształcając równanie współczynnika wykorzystania energii wiatru patrz tutaj z postaci C_p = ƒ(V, V₀) na postać V₀ = ƒ(C_p, V) . Rozwiązując otrzymaną tym sposobem funkcję, okazuje się, że posiada ona trzy rozwiązania V₀₁(7), V₀₂ (8) oraz V₀₃(9):

(7)

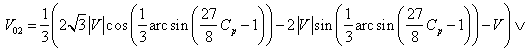(8)

(9)

Analizując otrzymane rozwiązania przyjęto, że dziedzinę funkcji V₀ = ƒ(C_p, V) w przypadku argumentu C_p stanowi zbiór liczb z zakresu 〈0, 0.5〉, natomiast dla argumentu V zbiór liczb 〈0, 22〉. Funkcja dla tak zdefiniowanej dziedziny w przypadku rozwiązania V₀₁ (7) oraz V₀₃ (9) przyjmuje tylko wartości ujemne (rys 2), przez co nie ma fizycznego sensu. Natomiast rozwiązanie V₀₂ (8) przyjmuje tylko wartości dodatnie (rys 2), dlatego też wzór na prędkość wiatru za kołem wiatrowym przyjmuje postać (8).

Rys. 2. Wykres zbioru wartości funkcji a) V₀₁ (7); b) V₀₂ (8); c) V₀₃ (9) dla argumentów C_p ∈ 〈0,0.5〉 oraz V ∈ 〈0,22〉.

Po zdefiniowaniu siły bocznej F_T działającej na ster tylni (2) można określić, ile wynosi moment obrotowy pochodzący od tego elementu elektrowni wiatrowej. Przy długości ramienia siły wynoszącej l_t wartość tego momentu równa się (10):

(10)

Jak wynika z rys 3 długość ramienia siły l_t odmierzana jest od osi obrotu gondoli do punktu środka parcia wiatru na ster tylni. W skład tak zdefiniowanego odcinka wchodzą dwie składowe. Pierwsza z nich to długość ramienia, na którym zamontowany jest ster tylni l_t1 (w modelu przyjęto, że jest ona równa średnicy koła wiatrowego D). Druga związana jest ze środkiem parcia wiatru na ster tylni i wynosi V_t2. Zatem całkowita długość ramienia siły wyniesie (11):

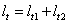(11)

Punkt przyłożenia wypadkowej siły aerodynamicznej działającej na ster tylni (środek parcia) zmienia swe położenie w zależności od kąta natarcia wiatru Θ. Natomiast długość odcinka l_t zmienia się wraz ze zmianą środka parcia wiatru i wynosi (12):

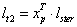(12)

gdzie:

xpT - współczynnik położenia środka parcia, lster - długość steru tylnego.

Rys. 3. Siły aerodynamiczne, występujące na kole wiatrowym odchylonym od kierunku wiatru (Θ - kąt odchylenia osi wirnika od kierunku wiatru, Θ_z - położenie osi wirnika, Θ_wiatr- kierunek wiania wiatru, F_T - siła boczna wywierana przez wiatr na ster tylni, F_X, F_Y - składowe siły parcia wiatru na koło wiatrowe, V - prędkość wiatru, V_X i V_Y - składowe prędkości wiatru, V₀ - prędkość wiatru za kołem wiatrowym,V_0X i V_0X - składowe prędkości wiatru za kołem wiatrowym z - prędkość kątowa elektrowni względem osi pionowej Z, l_t1 i l_t2 - ramie siły F_T, l_ster - długość płata steru tylnego, l_x - ramie siły F_X , l_y - ramie siły F_Y).

W publikacji [1] przedstawiono wykres położenia środka parcia dla płyt płaskich o różnych wydłużeniach λ_w (również dla profilu o wydłużeniu λ_w = 0.5). Na potrzeby modelu matematycznego wybrano kilka charakterystycznych punktów z tej charakterystyki. Tak otrzymany zbiór punktów wykorzystano następnie do aproksymacji. Program Matlab posiada wiele funkcji pozwalających na aproksymację punktową, jedną z nich jest funkcja polifit(). Podczas aproksymacji całej charakterystyki jednym wielomianem za pomocą tej komendy okazało się, że niemożliwe jest otrzymanie zadowalającego rozwiązania - błąd aproksymacji w skrajnych przypadkach osiągał nawet wartość 10% wartości rzeczywistej. Związku z tym podzielono zbiór punktów na dwa podzbiory i dokonano oddzielnej aproksymacji charakterystyki dla argumentów z przedziału 〈0,0.28〉 oraz dla argumentów z przedziału 〈0.28,1.06〉. Cały skrypt dokonujący aproksymacji charakterystyki położenia środka parcia umieszczono w zakładce Initialization w masce podsystemu ”MODEL STERU TYLNEGO ZE STEROWANIEM”.

Na rys 4przedstawiono wynik przeprowadzonej aproksymacji. Jak widać, praktycznie wszystkie punkty wykorzystane do tego celu przechodzą przez funkcję aproksymującą (wartość błędu aproksymacji mieści się w granicy +/-0.5% wartości rzeczywistej).

Rys. 4. Wynik aproksymacji charakterystyki położenia środka parcia x_p^T (dla płyty płaskiej o wydłużeniu λ_w=0.5) w funkcji kąta natarcia wiatru Θ z zaznaczeniem punktów użytych do aproksymacji.