Wytwarzanie energii elektrycznej przez elektrownię wiatrową jest optymalizowane dla pewnych prędkości wiatru mieszczących się w granicach 10-13m/s. W przypadku silniejszych wiatrów w turbozespołach nieposiadających odpowiednich układów sterowania dochodzi do przeciążenia generatora, czego konsekwencją może być jego uszkodzenie. Dlatego też, aby całkowicie wykorzystać potencjał wiatru, tworzy się układy sterowania, które sprawiają, że przy silniejszych podmuchach turbina wiatrowa pobiera mniej energii z wiatru. Jednym ze sposobów takiej regulacji jest odchodzenie elektrowni od wiatru. Ten rodzaj regulacji często wykorzystywany jest w siłowniach wiatrowych wyposażonych w ster tylni, ponieważ w takim przypadku jest to najtańsze rozwiązanie. Ten sposób regulacji wykorzystano również w modelu matematycznym. Na rys. 1 przedstawiono sytuację, kiedy przy zbyt silnym wietrze dochodzi do pewnego odchylenia steru tylnego od osi wirnika Θ_z o kąt Θ_t .

Rys. 1. Siły aerodynamiczne, występujące na kole wiatrowym przy pewnym odchyleniu steru tylnego (Θ - kąt odchylenia osi wirnika od kierunku wiatru, Θ_z - położenie osi wirnika, Θ_wiatr- kierunek wiania wiatru, Θ_ster - położenie steru tylnego, Θ_t - kąt odchylenia steru tylnego od osi wirnika, F_T - siła boczna wywierana przez wiatr na ster tylni, F_X, F_Y - składowe siły parcia wiatru na koło wiatrowe, V - prędkość wiatru, V_X i V_Y - składowe prędkości wiatru, V₀ - prędkość wiatru za kołem wiatrowym, V_0X i V_0X - składowe prędkości wiatru za kołem wiatrowym z - prędkość kątowa elektrowni względem osi pionowej Z, l_t1 i l_t2 - ramie siły F_T, l_ster - długość płata steru tylnego, l_x - ramie siły F_X , l_y - ramie siły F_Y).

Jak wynika z rys. 1, kąt natarcia wiatru na ster tylni nie jest równy kątowi odchylenia osi wirnika od kierunku wiatru Θ, ponieważ zwiększa się jeszcze o kąt odchylenia steru tylnegoΘ_t. W takiej sytuacji należy dokonać korekty równania patrz tutaj, które przekształci się do te postaci (1):

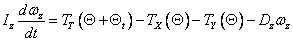(1)

gdzie:

Θt - kąt odchylenia steru tylnego od osi wirnika.

Najprostszym sposobem na regulację wychylenia steru tylnego jest wykorzystanie do tego zwykłego siłownika. Pracą tego urządzenia może sterować zwykły mikrokontroler, który na podstawie otrzymanych danych takich jak prędkość wiatru, czy też wartość mocy wytwarzanej przez generator zadawałby odpowiednie wychylenie siłownikowi. Innym rozwiązaniem jest zastosowanie sterownika programowalnego PLC zamiast mikrokontrolera. Zdecydowanie zwiększa to niezawodność układu sterowania, jednocześnie pozwala na szerszą integrację z innymi układami systemu. W obu konfiguracjach najważniejszą rzeczą jest stworzenie odpowiedniego algorytmu, który na podstawie danych wejściowych generowałby odpowiedni sygnał sterujący. W obecnych czasach układy elektroniczne są na tyle szybkie, że pozwalają na wykorzystanie skomplikowanych obliczeniowo algorytmów sterowania. Jedne z nich to algorytmy, które w swoim działaniu wykorzystują elementy logiki rozmytej. Ten rodzaj algorytmów pozwala na zaimplementowanie wiedzy eksperckiej oraz często okazuje się najlepszym rozwiązaniem w przypadku obiektów sterowania, w których występują silne nieliniowości. Ze względu na te zalety postanowiono wykorzystać sterowanie rozmyte w modelowanym układzie.

Przed przystąpieniem do formułowania bazy reguł określono, jakie dane wejściowe będą wykorzystywane w procesie sterowania, tak więc sygnał wyjściowy będzie generowany na podstawie:

Wielkość mierzona przez urządzenie pomiarowe, jak i sygnał wyjściowy z tego urządzenia są zazwyczaj pewnymi funkcjami czasu. Dlatego przy modelowaniu elektrowni wiatrowej należałoby uwzględnić dynamikę wiatromierza. Jednak w związku z tym, że w stworzonym modelu nie bierze się pod uwagę stochastycznego charakteru wiatru, zdecydowano się pominąć dynamikę tego elementu.

Natomiast przy modelowaniu pracy elementu wykonawczego, jakim jest siłownik, posłużono się informacją, że urządzenie to realizuje wychylenie steru tylnego z położenia znajdującego się wzdłuż osi wirnika Θ_z do położenia Θ_t = 90^o w czasie 20s. Dodatkowo przyjęto, że kąt wychylenia steru narasta liniowo.

Przed zdefiniowaniem zmiennych lingwistycznych oraz utworzeniem dla nich funkcji przynależności należało zorientować się, jaki wpływ na generowaną moc ma wychylenie steru tylnego. Analizując równanie na moc mechaniczną uzyskiwaną przez łopaty wirnika (patrz tutaj) oraz biorąc pod uwagę, że straty w procesie wytwarzania energii elektrycznej w modelowanym układzie wynikają głównie ze sprawności generatora , można zapisać, że moc wytwarzana przez generator jest równa (2) :

(2)

gdzie:

Pg – moc wytwarzana przez generator

Biorąc pod uwagę to, że wychylenie steru następuje tylko w momencie przekroczenia przez generator swoich wartości znamionowych. Innymi słowy przy większych prędkościach wiatru wychylenie steru powinno powodować, że wytwarzana moc generatora powinna oscylować wokół wartości znamionowej Pn. Jednocześnie przyjmuje się, że wielkość steru dobrano tak, że nie wywołuje on wychylenia elektrowni o kąt Θ większy niż 10^o oraz gęstość powietrza jest stała i wynosi 1,225kg/m². Zakłada się również, że współczynnik wykorzystania energii osiąga swoją wartość maksymalną C_p^max = 0.4, natomiast sprawność generatora wynosi η = 87.7%. Tak sformułowane warunki pozwalają wyznaczyć kąt odchylenia steru Θ_t w funkcji prędkości wiatru, przy którym turbozespół pracuje w warunkach znamionowych. Funkcja ta przyjmie postać (3):

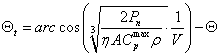(3)

Na rys. 2 przedstawiono rozwiązanie równania (3) dla przedziału prędkości wiatru V ∈ 〈12,17〉. Jak widać wykres ten przedstawia funkcję o małej nieliniowości (w praktyce można by ją aproksymować dwoma funkcjami liniowymi). Jednak należy pamiętać, że wyznaczono ją dla pewnych konkretnych warunków, które podczas rzeczywistej pracy elektrowni wiatrowej ulegają zmianom. Mimo to wykres ten daje pewne wyobrażenie tego powinno wynieść wychylenie steru przy danej prędkości wiatru, co stanowi pewną wiedzę ekspercką, która ułatwi tworzenie funkcji przynależności zbiorów oraz bazy reguł na potrzeby sterowania rozmytego.

Rys. 2. Odchylenie steru t w funkcji prędkości wiatru V, przy którym turbozespół pracuje w warunkach znamionowych.

Przy sporządzaniu funkcji przynależności dla poszczególnych wejść i wyjścia regulatora rozmytego posłużono się znajomością podstawowych zasad opisujących stan pracy generatora synchronicznego z magnesami trwałymi. Otóż założono że możliwe jest przeciążenie tej maszyny nie większe niż 20% wartości mocy znamionowej tego urządzenia. Dodatkowo praca podczas przeciążenia nie może trwać dłużej niż 3 minuty, po czym generator ten nie powinien przekraczać mocy znamionowej przez czas wynoszący czterokrotność czasu jego pracy w przeciążeniu.

Opisane powyżej informacje pozwoliły na stworzenie podziału poszczególnych dziedzin argumentów wejść i wyjścia regulatora rozmytego na zakresy określone przez zmienne lingwistyczne:

Następnie dla każdego zbioru rozmytego (zmiennej lingwistycznej) sporządzono odpowiednią funkcje przynależności określającą w jakim stopniu wartość danego argumentu przynależy do zmiennej lingwistycznej (rys. 3).

Rys. 3. Funkcje przynależności oraz odpowiadające im zmienne lingwistyczne dla: a) wejścia V - prędkość wiatru; b) wejścia P_p% - parametru przeciążenia; c) wejścia T_p - względnego czasu trwania przeciążenia; d) wyjścia, Θ_t - wychylenie steru tylnego.

Tak sporządzony podział argumentów wejść i wyjścia regulatora bazującego na logice rozmytej oraz utworzone dla nich funkcje przynależności pozwalają na sporządzenie bazy reguł, którymi kieruje się regulator przy wypracowywaniu odpowiedniej wartości zadanej. Reguły te przyjmują postać:

Na rys. 4 przedstawiono graficzną interpretację utworzonej bazy reguł. Wynika z niej to, że główne kryterium przy wyznaczaniu zadanego kąta odchylenia steru tylnego stanowi prędkość wiatru (4 pierwsze reguły). Natomiast dwa pozostałe parametry wejściowe, określające stan pracy generatora wywołują korektę tego położenia (reguły 5-10). Tak sporządzona baza reguł pozwala wykorzystać cały potencjał energetyczny wiatru, jednocześnie zabezpieczając generator przed nieprawidłową pracą.

Rys. 4. Graficzna interpretacja reguł.

Należy również zaznaczyć, że przy interpretacji reguł regulator rozmyty wykorzyrzystuje:

Aby model matematyczny dobrze opisywał pracę układu rzeczywistego, wypracowywana odpowiedź z regulatora rozmytego na podstawie danych wejściowych jest analizowana przez układ co okres czasu wynoszący 1s. Dzięki temu siłownik nie nadąża, cały czas za zmieniającą się w sposób dynamiczny zadaną wartością z regulatora, lecz dokonuje korekty położenia co 1s. Taki zabieg sprawia, że proces zużycia się tego elementu przebiega znacznie dłużej. Jednocześnie założono, że skok siłownika umożliwia zmianę położenia steru o dwa stopnie, tak więc odpowiedź z układu regulatora przyjmuje tylko parzyste wartości z przedziału od 0^o do 40^o.