Aby zobrazować wpływ zmiany kierunku wiania wiatru na parametry elektrowni wiatrowej, zdecydowano się przeprowadzić trzy symulacje. W pierwszej przy prędkości wiatru wynoszącej 8m/s, zmiana kierunku wiania wiatru dokonuje się przez okres 10s. W tym czasie położenie osi wiatru
Θwiatr zmienia się z 0
o do 30
o. Wyniki tej symulacji przedstawiono na
rys. 1. Jak się okazuje, przy takiej zmianie parametrów wiatru dochodzi do pewnej oscylacji mocy generowanej przez elektrownię wiatrową. Wahanie to jest konsekwencją przebiegu kąta odchylenia osi wirnika od kierunku wiatru
Θ, który determinuje wartość składowej prędkości wiatru prostopadłej do płaszczyzny koła wiatrowego
VX. Należy tu zaznaczyć, że tylko od tej składowej prędkości wiatru, turbina wiatrowa pozyskuje moc mechaniczną, którą następnie pobiera generator i przekształca na energię elektryczną. Zatem aby zrozumieć przyczynę występujących tu wahań mocy, należy przeanalizować przebiegi momentów obrotowych, które decydują o dynamice zmian położenia osi wirnika
Θz względem osi wiatru
Θwiatr. Inaczej ujmując, mają bezpośredni wpływ na wartość kąta
Θ. W początkowej fazie symulacji układ znajduje się w punkcie równowagi, w którym momenty obrotowe, próbujące ustawić turbinę wiatrową w położeniu za wieżą
TX,
TY (wywołane siłą parcia wiatru na koło wiatrowe) równoważone są przez moment obrotowy
TT (pochodzący od siły parcia wiatru na ster tylni). Zatem można zapisać
(1):
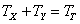 |
(1) |
Należy również zaznaczyć, że uzyskany przez układ punkt równowagi osiągnięty został dla dodatniego odchylenia osi wirnika od kierunku wiatru Θ równego około 10o. Natomiast w momencie, kiedy następuje zmiana kierunku wiania wiatru, położenie osi wiatru Θwiatr wzrasta, zbliżając się do położenia osi wirnika Θz. Zatem kąt odchylenia Θ maleje, co powoduje utratę przez układ punktu równowagi. Wobec tego można zapisać (2):
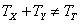 |
(2) |
Powyższe wyrażenie oznacza, że występujące w układzie momenty obrotowe przy zmianie kierunku wiania wiatru przestają się równoważyć, co w rezultacie powoduje przyrost prędkości obrotowej turbozespołu w osi Z ωz. Spoglądając na dalszy przebieg prędkości można zauważyć, że po osiągnięciu przez oś wiatru Θwiatr położenia osi wirnika Θz (Θ = 0o) prędkość ta zaczyna maleć. Przyczyna takiego zachowania się układu jest oczywista i wiąże się z tym, że dla kąta Θ bliskiego 0o, opisane w podrozdziałach tutaj i tutaj siły, wywołujące obrót elektrowni wiatrowej w osi Z są bardzo niewielkie. Dlatego pochodzące od nich momenty obrotowe wynoszą praktycznie zero. Natomiast współczynnik tłumienia dla ruchu obrotowego elektrowni wiatrowej w osi Z jest dość duży. Konsekwencją tych dwóch rzeczy jest niewielki spadek prędkości, który trwa, aż do momentu kiedy wystąpi na tyle duże odchylenie Θ, że występujące siły zniwelują efekt tłumienia prędkości obrotowej. W kolejnym etapie nadążania elektrowni wiatrowej za zmianą kierunku wiania wiatru dochodzi do jednostajnego przyrostu położenia osi wirnika Θz, które z czasem ponownie zbliża się do osi wiatru. Jednak należy tu zaznaczyć, że w tym przypadku układ nie osiąga stanu, w którym odchylenie Θ = 0o. Skutkiem tego układ stabilizuje się przy ujemnych wartościach odchylenia Θ. Tym samym przeprowadzona symulacja ukazuje, że elektrownia wiatrowa posiada dwa stabilne punkty pracy: pierwszy przy dodatnim kącie natarcia wiatru Θ (10o) oraz drugi przy kącie natarcia wiatru (-4o). Należy również zaznaczyć, że wartości bezwzględne tak zdefiniowanych odchyleń nie są jednakowe. Związane jest to z tym, że charakterystyka aerodynamicznego współczynnika Cy w funkcji kąta natarcia wiatru nie jest parzysta, co powoduje, że dla dodatnich kątów Θ moment obrotowy pochodzący od siły FY (jej wartość zależy od współczynnika Cy) jest znacznie większy niż dla kątów ujemnych. W konsekwencji tego moment obrotowy pochodzący od steru tylnego musi być znacznie większy dla dodatnich kątów natarcia wiatru, aby wypadkowa momentów mechanicznych w osi Z wyniosła zero.
Rys. 1. Wyniki symulacji przy zmianie kierunku wiania wiatru (Vhub=8m/s, Θzm=30o, Tzm =10s): a) Θ- kąt odchylenia osi wirnika od kierunku wiatru, Θz - położenie osi wirnika, Θwiatr - kierunek wiania wiatru, b) V- prędkość wiatru, VX - składowa prędkości wiatru prostopadła do koła wiatrowego, c) ωz- prędkość kątowa elektrowni względem osi pionowej Z, d) ωw - prędkość obrotowa wału turbiny, e) TT - moment obrotowy wywołany siłą parcia wiatru na ster tylni, TX, TY - moment obrotowy wywołany siłą parcia wiatru na koło wiatrowe, e) Pg - moc generatora, Pmech - moc mechaniczna turbiny wiatrowej.
Kolejną symulację wykonano przy identycznych parametrach wiatru z tą różnicą, że kąt zmiany kierunku wiania wiatru zwiększono dwukrotnie. Natomiast wyniki zamieszczono na rys. 2. Na pierwszy rzut oka otrzymane przebiegi nieznacznie różnią się od tych uzyskanych w poprzedniej symulacji. Jednak podczas głębszej analizy okazuje się, że jednak występują znaczące różnice. Po pierwsze prędkość obrotowa elektrowni wiatrowej w osi Z wzrosła ponad trzykrotnie, osiągając w pewnym momencie wartość 0.18 rad/s. Należy tu zaznaczyć, że nie powinno się dopuszczać do prędkości większych od 0.31 rad/s co związane jest z powstającymi wtedy dużymi siłami giroskopowymi próbującymi złamać płaty wirnika u ich podstawy. Po drugie w przeciwieństwie do poprzedniej symulacji po zmianie parametrów wiatru układ nie osiąga ostatecznie punktu równowagi przy ujemnym kącie odchylenia Θ. Spowodowane jest to tym, że układ w 21s symulacji siłą bezwładności przechodzi przez położenie, dla którego odchylenie Θ= 0o. W konsekwencji wchodzi w obszar pracy przy dodatnich kątów odchylenia Θ i ostatecznie osiąga ten sam punkt równowagi, z którego startował, co powoduje większe wahania w generowanej mocy w porównaniu z poprzednią symulacją.
Rys. 2. Wyniki symulacji przy zmianie kierunku wiania wiatru (Vhub=8m/s, Θzm=60o, Tzm =10s): a) Θ- kąt odchylenia osi wirnika od kierunku wiatru, Θz - położenie osi wirnika, Θwiatr - kierunek wiania wiatru, b) V- prędkość wiatru, VX - składowa prędkości wiatru prostopadła do koła wiatrowego, c) ωz- prędkość kątowa elektrowni względem osi pionowej Z, d) ωw - prędkość obrotowa wału turbiny, e) TT - moment obrotowy wywołany siłą parcia wiatru na ster tylni, TX, TY - moment obrotowy wywołany siłą parcia wiatru na koło wiatrowe, e) Pg - moc generatora, Pmech - moc mechaniczna turbiny wiatrowej.
Trzecią symulację przeprowadzono dla tych samych parametrów co w pierwszej, zwiększając jedynie prędkość wiatru do wartości Vhub=12.1m/s, przy której generator osiąga wartości bliskie znamionowych (rys. 3). Zwiększenie siły wiatru spowodowało, że w przebiegach mocy generatora występują największe oscylacje. Bezpośredni wpływ na to ma wielkość momentów, wywołujących obrót elektrowni wiatrowej w osi Z. Dla tej symulacji momenty te po osiągnięciu stabilnego punktu pracy wynoszą kolejno TT = 65Nm, TX = 10Nm, TY = 55Nm, przez co są trzykrotnie większe niż w przypadku pierwszej symulacji. Powoduje to powstanie oscylacji podczas osiągania przez elektrownię wiatrową punktu pracy, w której wypadkowa momentów obrotowych w osi Z jest równa zero.
Rys. 3. Wyniki symulacji przy zmianie kierunku wiania wiatru (Vhub=12m/s, Θzm=30o, Tzm =10s): a) Θ- kąt odchylenia osi wirnika od kierunku wiatru, Θz - położenie osi wirnika, Θwiatr - kierunek wiania wiatru, b) V- prędkość wiatru, VX - składowa prędkości wiatru prostopadła do koła wiatrowego, c) ωz- prędkość kątowa elektrowni względem osi pionowej Z, d) ωw - prędkość obrotowa wału turbiny, e) TT - moment obrotowy wywołany siłą parcia wiatru na ster tylni, TX, TY - moment obrotowy wywołany siłą parcia wiatru na koło wiatrowe, e) Pg - moc generatora, Pmech - moc mechaniczna turbiny wiatrowej.

