Proces wyznaczania zadawanego momentu mechanicznego silnika, wykonuje się w podobny sposób jak w modelu matematycznym opisanym
tutaj. Występują jednak pewne różnice wynikające z charakteru tworzonych modeli (ciągły w programie Matlab, dyskretny na stanowisku laboratoryjnym) oraz będące skutkiem pominięcia niektórych dynamik w modelu laboratoryjnym. Do zobrazowania tych różnic wykonano schemat układu zadawania momentu, który przedstawiono na
rys. 1.
Rys. 1. Schemat układu zadawania momentu mechanicznego na wał silnika indukcyjnego z zaznaczeniem nazw zmiennych użytych w programie sterującym.
Z powyższego rysunku wynika, że w modelu laboratoryjnym pominięto dynamikę steru tylnego. Wiąże się to z jej złożonym charakterem oraz brakiem możliwości przedstawienia dynamiki odchylania się elektrowni wiatrowej od wiatru w przypadku silnych podmuchów (użyta przekładnia nie pozwala osiągnąć znamionowych parametrów generatora). Zdecydowano się również na ograniczenie liczby opcji, pozostawiając tylko te, które opisują parametry wiatru podczas normalnych warunków wiatrowych. Pozwala to przeprowadzić badania podczas:
- stałej prędkości wiatru (OPCJA=1),
- podmuchu koherentnego (OPCJA=2), zdefiniowanego identycznie jak w modelu matematycznym z tą różnicą, że podczas przeprowadzania badań można go wielokrotnie wywoływać i jednocześnie dokonywać zmian jego parametrów,
- podmuchu wiatru (OPCJA=3), który różni się od tego z modelu matematycznego tym, że występuje cyklicznie co pewien okres czasu, a jego parametry można dynamicznie zmieniać w trakcie przeprowadzanych badań.
Dokładny opis zmiennych definiujących poszczególne warunki wiatrowe w modelu laboratoryjnym przedstawiono na rys. 1.
Kolejnym krokiem jak wynika z rys. 1 jest wyznaczenie wartości współczynnika wykorzystania energii wiatru Cp na podstawie wyróżnika szybkobieżności λ, którego wartość jest wprost proporcjonalna do prędkości obrotowej koła wiatrowego. Dlatego też wykorzystuje się przefiltrowany sygnał z obserwatora prędkości, który najpierw przelicza się z jednostek względnych na jednostki wyrażane w rad/s, a następnie dzieli przez wartość przekładni. Tak otrzymane wyrażenie definiuje się jako prędkość obrotową modelowanego silnika wiatrowego ωw. Pozwala to obliczyć moc mechaniczną pozyskiwaną z wiatru przez silnik wiatrowy zgodnie ze wzorem patrz tutaj.
Z kolei transmitancję opisującą dynamikę konwersji energii wiatru na energię mechaniczną koła wiatrowego (patrz tutaj) ze względu na jej implementację w układzie cyfrowym należało zdyskretyzować. W tym celu posłużono się regułą trapezów, która pozwala na podstawie znajomości transmitancji ciągłej G(s) wyznaczyć równoważną transmitancję dyskretną G(z), dokonując podstawienia (1):
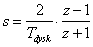 |
(1) |
gdzie: |
Tdysk - okres próbkowania, który w przypadku użytego w przekształtniku procesora sygnałowego wynosi Tdysk = 150μs |
Otrzymaną tym sposobem dyskretną transmitancję dynamiki koła wiatrowego przedstawiono na rys. 1. Pozwala ona wyznaczyć dyskretne równanie stanu, które w prosty sposób można zaimplementować w programie sterującym. Tak opisana zależność przybiera postać (2):
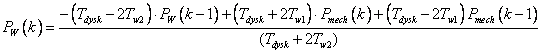 |
(2) |
W kolejnym etapie wyznaczania zadawanego momentu mechanicznego uwzględnia się efekt mechanicznych kołysań mocy, które definiuje się zależnościami przedstawionymi tutaj. W równaniach tych występuje zmienna, której wartość zależy od położenia kątowego wału turbiny. Tak więc dokonano estymacji tego parametru, przyjmując najpierw założenie, że prędkość obrotowa modelowanego silnika wiatrowego ωw pomiędzy dwoma kolejnymi okresami impulsowania jest stała. Pozwala to wyznaczyć położenie wału turbiny ze wzoru (3):
 |
(3) |
Ostatnim elementem opisującym przemianę energii kinetycznej wiatru na energię mechaniczną koła wiatrowego jest dynamika układu przeniesienia napędu, na którą największy wpływ ma bezwładność koła wiatrowego. W związku z tym, że wartość wytwarzanego momentu elektromagnetycznego Tg przez generator nie jest dostępna w modelu laboratoryjnym, podejście do zamodelowania tej dynamiki przedstawione w tutaj jest niewykonalne. Tym samym zdecydowano się rozwiązać ten problem, przyrównując dynamikę układu przeniesienia napędu do transmitancji w postaci inercji pierwszego rzędu ze stałą czasową TJ (4).
 |
(4) |
Wyznaczenie wartości stałej dokonano w sposób eksperymentalny, porównując otrzymane przebiegi czasowe wytwarzanej mocy generatora podczas identycznych podmuchów wiatru, z przebiegami otrzymanymi z symulacji na modelu matematycznym.
Podobnie jak w przypadku transmitancji dynamiki koła wiatrowego dokonano jej dyskretyzacji, w konsekwencji otrzymując równanie stanu (5):
 |
(5) |
gdzie: |
Pwwbezl - moc mechaniczna koła wiatrowego po uwzględnieniu bezwładności koła wiatrowego. |
Po podzieleniu mocy mechanicznej uzyskiwanej przez turbinę wiatrową Pwwbezl, przez prędkość obrotową silnika indukcyjnego ωsil otrzymuje się wartość zadanego momentu mechanicznego wyrażonego w Nm. Następnie przelicza się go na jednostki bazowe, otrzymując ostatecznie zmienną x12, która jest zmienną sterowania multiskalarnego.

