Moc mechaniczna pozyskiwana z wiatru przez koło wiatrowe zgodnie ze zdefiniowanym wcześniej wzorem wynosi
(1):
 |
(1) |
Występujący w równaniu (1) współczynnik wykorzystania energii wiatru Cp dla potrzeb modelowania matematycznego określa się zazwyczaj jako funkcję argumentu wyróżnika szybkobieżności λ. Argument ten definiuje się wzorem (2):
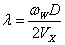 |
(2) |
gdzie: |
ωW - prędkość kątowa koła wiatrowego. |
Kształt charakterystyki Cp(λ) dla turbin wiatrowych o poziomej osi obrotu zależy głównie od liczby wykorzystanych łopat. Zatem charakterystyki te są bardzo zbliżone dla danego typu koła wiatrowego. W przypadku wykorzystania sterowania pitch control zmienia się ona również wraz ze zmianą kąta nachylenia łopat ∂. Wówczas na potrzeby modelu matematycznego tworzy się rodzinę takich charakterystyk dla różnych kątów ∂.
Na rys. 1 pokazano przykładowy kształt charakterystyki Cp(λ), którą sporządzono dla duńskiej turbiny wiatrowej Vestas o mocy 55 kW [8]. Jak widać współczynnik mocy osiąga swoje maksimum dla wyróżnika szybkobieżności równego 5.2, co odpowiada współczesnym turbinom wiatrowym, w których punkt ekstremum wypada właśnie dla takiego wyróżnika szybkobieżności. Dlatego też zdecydowano się wykorzystać tą charakterystykę w modelu matematycznym. Podobnie jak w przypadku innych charakterystyk dokonano jej aproksymacji za pomocą funkcji polifit() w Matlabie, a skrypt umieszczono w masce podsystemu ”MODEL KOŁA WIATROWEGO”. Aby osiągnąć jak lepszy rezultat, podzielono dziedzinę charakterystyki na dwa podzbiory i aproksymowano ją za pomocą dwóch wielomianów piątego rzędu.
Rys. 2. Charakterystyka współczynnika wykorzystania energii wiatru w funkcji wyróżnika szybkobieżności dla duńskiej turbiny wiatrowej VESTAS o mocy 55 kW z zaznaczeniem punktów użytych do aproksymacji charakterystyki.
Podczas konwersji energii wiatru na energię mechaniczną turbiny wiatrowej dochodzi do złożonych zjawisk aerodynamicznych, przy modelowaniu których wykorzystuje się m.in. teorię elementów płata oraz model przestrzenny wiatru. Takie podejście wymaga znajomości charakterystyki aerodynamicznej profilu płata oraz prowadzi do wyprowadzenia złożonych, nieliniowych równań różniczkowych. W publikacji [3] przedstawiono, że model dynamiki koła wiatrowego można znacznie uprościć, opisując go, podobnie jak w przypadku turbin parowych bądź wodnych za pomocą transmitancji (3):
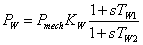 |
(3) |
gdzie: |
KW - współczynnik wzmocnienia,
Tw1, Tw2 - stałe czasowe. |
Parametry transmitancji, jak podano [3] dla średniej elektrowni wiatrowej wykorzystującej regulację typu stall przyjmują wartość KW = 1, Tw1 = 3.3 s, Tw2 = 0.9 s. Ponieważ modelowana elektrownia wiatrowa jest mocy 8.5 kW, zachodzące w niej zjawiska aerodynamiczne przebiegają znacznie szybciej niż w przypadku średniej elektrowni wiatrowej. Z tej przyczyny zdecydowano się przyjąć: KW = 1, Tw1 = 0.8 s, Tw2 = 0.45 s.
Podobnie jak w przypadku innych podsystemów modelu, dla tego elementu również stworzono okno dialogowe (rys. 3), które umożliwia zmianę stałych czasowych dynamiki koła wiatrowego.
Rys. 3. Okno dialogowe maski podsystemu ”MODEL KOŁA WIATROWEGO”.


